Я пришёл к выводу, что единственная возможность подойти к проблеме изучения величин ошибок, при вычислении количества простых чисел на интервалах (0,m). Это представление значения (m), как суммы арифметической прогрессии
I came to the conclusion that the only way to approach the problem of studying the errors in calculating the number of primes in the intervals (0, m). This is a representation of the value (m), as the sum of an arithmetic progression
The formula for calculating the number of primes in the intervals
Update: If the value of
the calculation error does not exceed P_n
Clarifying formula supplements:
Sergey Sitnikov
I came to the conclusion that the only way to approach the problem of studying the errors in calculating the number of primes in the intervals (0, m). This is a representation of the value (m), as the sum of an arithmetic progression
value
makes it possible to understand how errors occur in the calculation and purposefully change the errors by changing the value realizedUpdate: If the value of
Clarifying formula supplements:
Sergey Sitnikov
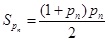
Комментариев нет:
Отправить комментарий