Have. Formula algorithm sieve of Eratosthenes
So, we have the formula algorithms sieve of Eratosthenes for (N) numbers, for Prime numbers and composite numbers:
What actions can be performed with formulas algorithms, and which of these actions lead to the natural result, and which lead to Molech. By the way, a similar problem, and the "Test the ingenuity"
For example, the addition of the
I will show you a slightly different approach in the search for the ideal formula of the algorithm.
We denote for the convenience of the formula algorithm primes through (x)
If we suppose that in the interval
all of a number (N), Prime numbers. The formula of the algorithm will have the formSo, we have the formula algorithms sieve of Eratosthenes for (N) numbers, for Prime numbers and composite numbers:
What actions can be performed with formulas algorithms, and which of these actions lead to the natural result, and which lead to Molech. By the way, a similar problem, and the "Test the ingenuity"
For example, the addition of the
leads to the natural result.
Division
formulas for (N) numbers, the formula of the algorithm of Prime numbers, gives us the formula of the algorithm for Prime numbers, but the sample is not the simple basic numbers and composite multiples of simple basic numbers. And the sample is as integral as the reference numbers and the next integral multiple of, the initial (basic) composite numbers. In General, this is an example of Moloch.
But do a little differently, the formula of the algorithm, which gives the number of primes with minimum calculation error is within
But do a little differently, the formula of the algorithm, which gives the number of primes with minimum calculation error is within
Within these limits is the formula of the algorithm described in the previous message «Chernovik formula» in Addition to the values for the three initial (n)
But be in the range of the search, is necessary but not enough.I will show you a slightly different approach in the search for the ideal formula of the algorithm.
We denote for the convenience of the formula algorithm primes through (x)
The attitude of the formula algorithm composite numbers to the formula of the algorithm of Prime numbers is the value of the average gap between the simple numbers on the interval
minus one.
But if we assume and accept that the relationship is always equal to the average gap between the simple numbers on the interval
will have the form
Compare with the formula
Formula one gives an error of calculation, as a positive number, the second formula gives the error of calculation of a negative number.





















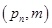


Комментариев нет:
Отправить комментарий