The quantity of primes at small intervals
S.V. Sitnikov
Annotation.
First non-snap formula of prime numbers calculation at small intervals.
Algorithmic formula of the Sieve of Eratosthenes. The possibility to solve complex problems with help of elementary methods (the quantity of primes at small intervals).
Key words: interval, prime/prime number, Sieve of Eratosthenes.
1
Sieve of Eratosthenes is an algorithm of finding all prime numbers up to certain whole number.
We derive algorithmic formula
Algorithmic formula (1,1) of Sieve of Eratosthenes
–prime/prime numbers
(n) –the number of a prime
The formula of finding the quantity of prime numbers at the intervals.
For example:
Miscalculation is a complex problem which is to be solved.
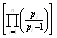 берётся только по целым числам
берётся только по целым числам
Но если взять за критерий оценки формулы не величину погрешности вычисления, а количество смены знаков у величин погрешности при вычислениях.
Есть интересный результат. Коэффициент 2,4
k=2,4
(E+-) - Количество смены знаков у величин погрешности при вычислении по формуле (1,4).
Значение в знаменателе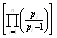 берётся только по целым числам
берётся только по целым числам Например: Для интервала (1,x) x=1299709. При коэффициенте
(к)=2,4 (E+-)=151
2
The distance between neighboring prime numbers.
The numerical segment between neighboring prime numbers.
We shall give four definitions:
1. Initial interval/segment.
2. Basis number.
3. Base set of the basis number.
4. The special form of the initial segment.
1. The initial interval is a segment which consists of basis numbers and their base sets/ bases.
which consists of basis numbers and their base sets/ bases.2. The basis number is a prime number (p).
3. The bases from the prime number (p) are all multiple numbers (p) without crossing numbers with their previous bases. The basis numbers is included to base set/or basis.
4. The special form of the initial is a segment similar and equal to the initial interval. It is equal to the initial interval by the quantity of all bases` elements, but the arrangement of basis numbers at it is different.
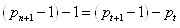
The segment
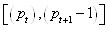 could be written as an initial interval but with different initial arrangement of basis numbers. Thereto we arrange numbers into prime factors beginning with the number
could be written as an initial interval but with different initial arrangement of basis numbers. Thereto we arrange numbers into prime factors beginning with the number  The smaller prime number is taken as a basis number. The rest numbers of the segment multiple to basis number are to be taken as its base set/ basis. In the same way just proceed to the next composite number which is not included into the previous basis, and so on. As a result, we obtain the special form of the interval from the segment
The smaller prime number is taken as a basis number. The rest numbers of the segment multiple to basis number are to be taken as its base set/ basis. In the same way just proceed to the next composite number which is not included into the previous basis, and so on. As a result, we obtain the special form of the interval from the segment 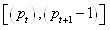
Firstly, we should check if there is any possibility for the special form interval to exist.
We interchange basis numbers on the segment  That is, we would try to make the special form interval from the initial segment
That is, we would try to make the special form interval from the initial segment 
When interchanging two basis numbers on the initial segment the values and their bases on the initial segment would be changed as well. We have:
1 the increase of basis with large basis numbers, and
2 simultaneous decrease of basis with small basis numbers.
The contrary arrangement is impossible because it would mean returning back to the initial state, returning to the initial segment. Bases change equally, with the same amount, but basis numbers are different in magnitude. It means that in first case, basis elements will be lost more, than gained in the second case. The quantity of all bases` elements in total amount will decrease at the interval.
When continuing changing positions of basis numbers we will reduce the quantity of elements of all bases. Hence, it is impossible to create special form of the interval similar and equal to the initial segment but with different arrangement of numbers. On the special form of the interval the quantity of elements of all bases will be less. But that won’t be a special form of the interval.
Thus, we have proved that there is no special form of the interval.
Hence:
It is a proof that at the interval
 always
always
Cited literature:
[1] А. И. Бородин. Теория чисел. Киев. 1992. (Borodin A.I.: Theory of numbers. Kiev
[2] И. Г. Башмакова. Ю. А. Белый. С. С. Демидов. Б. А. Розенфельд. А. П. Юшкевич. Хрестоматия по истории математики. Москва. 1976. (Bashmakov I.G, Belyi Y.A., Demidov S.S., Rosenfeld B.A., Yushkevich A.G.: Chrestomathy on the History of Mathmatics, Moscow, 1976)
[3] Д. Пойа. Математическое открытие. Перевод с английского В. С. Бермана. Под редакцией И. М. Яглома. Москва. 1976.(Poya D.: Mathematical discovery. Translated from English by Berman V.S. Edited by Yagloma I.M. Moscow, 1976)
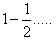
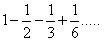
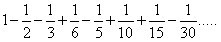
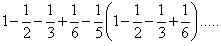




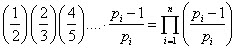
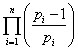
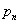

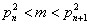

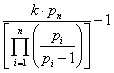
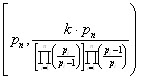


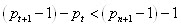

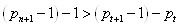

Комментариев нет:
Отправить комментарий