Number of primes in the interval (general formula);Количество простых чисел на интервале (Общая формула)
- формула вычисления результата решета Эратосфена
- формула среднего пробела между простыми числами
P_n - простое число
(n) - номер простого числа
Эти три значения имеют между собой прямую зависимость, изменение одного из них, влечёт за собой изменение двух других значений.
Ввожу новое обозначение. Символ \[n \not\to \infty \] - (n) не стремиться к бесконечности
Дело в том что:
Вопросы распределения простых чисел, изучаются элементарными методами и методом математического анализа. Все элементарные методы можно описать, как попытку установить бесконечность количества простых чисел в той или иной части натуральных ряда. То есть среди натуральных чисел того или иного определённого вида. Методы математического анализа берут начало с тождества Эйлера
На основании этого тождества вопросы распределения простых чисел приводятся к изучению специальной так называемой дзета-функции определяемой рядом
То есть проблема математического анализа нахождение достаточно простой аналитической функции f(x)
Асимптотически равной
Другими словами, искомая аналитическая функция f(x)
Должна быть приближённым выражением функции
Со сколь угодно малой относительной погрешностью при достаточно больших значениях (x)
Ещё проще, занимаемся не проблемой простых чисел, а проблемой, которая есть приближённое выражение проблемы простых чисел.
А теперь главное. Моя работа не является проблемой, которая является приближённым выражением проблемы простых чисел. Моя работа, есть сама проблема простых чисел, она самодостаточна. Что это значит?
Мне нет нужды в моей работе, обращаться за помощью к асимптотическим равенствам.
И что бы, не возник соблазн обратиться к асимптотическим равенствам, я ввожу новое обозначение.
(n) – не стремиться к бесконечности. Это символ \[n \not\to \infty \]
Символ \[n \not\to \infty \] означает, (n) – все действительные числа, но какой бы величины не было число (n), оно всегда есть конкретное число.
После этого вступления, можно заниматься (проблемой погрешности вычисления), при вычислении количества простых чисел на интервале.
Но это уже будет другая работа.
Sergey Sitnikov






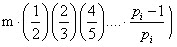

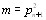
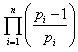




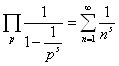
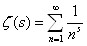

Комментариев нет:
Отправить комментарий